Programmation des réseaux de neurones sous Scilab

Scilab offre beaucoup de facilités pour programmer des algorithmes comportant des opérations sur les matrices. Pour optimiser un programme Scilab, Il faut éviter tant que c'est possibles les boucles ``while'', ``for'', et ramener les calculs effectués à des opérations sur des matrices. Au final, on a des programmes très compacts, qui s'exécutent à une vitesse comparable à celle d'un programme C. Les fonctions décrites ci- dessous implémentent la règle de rétropropagation sans utiliser de telles boucles. Voici les fonctions qui premettent de mettre en uvre l'algorithme de rétropropagation du gradient, décrit plus haut :

• Ceci est la fonction de transfert, qui est une tangente hyperbolique ramenée sur l'intervalle [0,1].

  function y = phi (x)
  
  // fonction de transfert couche cachée
  // à valeurs sur [0,1]
  
  	y= (1+tanh(x))/2;
  
  endfunction;
  

  remarque : l'argument x peut être un scalaire ou un vecteur.
• Dérivée de la fonction de transfert :

  function y = phi_prime(x)
  
  // derivee de la fonction de transfert couche cachée
  
  	y = 1-tanh(x).^2; 
  
  endfunction;
  

• La fonction init_perceptron permet d'initialiser un perceptron en fonction des bases d'entrée et de sortie 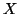$X$ et $Y$.

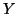  function net=init_perceptron(X,Y,n1,num_reseau)
  
  // X : base d'entree
  // Y : base de sortie
  // n1 : nb de neurones couche cachee
  // num_reseau : numero d'identification du reseau 
  
  	rand('normal'); // choix de la loi normale
  	rand('seed',num_reseau); // initialisation de la série aléatoire
  
  	[n0,K]=size(X);
  	[n2,K]=size(Y);
  
  	net.w1=rand(n1,n0)/sqrt(n0);
  
  	net.w2=rand(n2,n1)/sqrt(n1); 
  
  endfunction;
  

  remarques :
  • en Scilab, on ne déclare pas les variables. Dans une fonction, les variables qui ne sont pas les arguments de la fonction (en entrée ou en sortie) sont des variables locales. Les valeurs n0, K et n2 sont déduites de la taille des bases d'entrée et de sortie avec la fonction size.
  • L'objet net contient l'ensemble des caractéristiques du réseau. Dans le cas présenté, il contient les poids w1 et w2.
  • Les poids initiaux sont tirés selon une loi gaussienne. En supposant arbitrairement les entrées gaussiennes, on multiplie les matrices obtenues par les scalaire 1/sqrt(n0) et 1/sqrt(n1) pour ramener l'ecart-type de l'entrée des neurones proche de 1.
  Après initialisation, les matrices net.w1 et net.w2 contiennent les poids du réseau. la fonction propagation calcule la sortie du réseau en fonction de l'entrée qu'on lui applique.

  function y=propagation(net,x)
  
  // net : le reseau
  // x : vecteur d'entree
  
  	x1 = phi(net.w1*x);
  	y = net.w2 * x1;
  	
  endfunction;
  

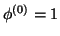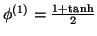  On remarquera que dans le modèle proposé, seule la couche cachée contient des unités non linéaires. On a donc littéralement $\phi^{(0)}=1$, $\phi^{(1)}=\frac{1+\tanh}{2}$ et $\phi^{(2)}=1$.
• La fonction retropropagation permet de modifier les poids du réseau, en fonction d'un couple de vecteurs (x,y) appartenant aux bases d'entrée et de sortie.

  function [net,err]=retropropagation(net,x,y,epsilon)
  
  // net : le reseau
  // x : vecteur d'entree
  // y : sortie desiree
  // epsilon : taux d'apprentissage
  
  	x1 = phi(net.w1*x);
  	x2 = net.w2 * x1;
  	
  // calcul des erreurs intermédiaires
  	
  	delta2=y-x2;
  	delta1=phi_prime(net.w1*x).*(net.w2'*delta2);
  	
  // rétropropagation	
  	
  	net.w2=net.w2+epsilon*delta2*x1';
  	net.w1=net.w1+epsilon*delta1*x';
  	
  // erreur moyenne
  
  	err=sqrt(delta2'*delta2);
  	
  endfunction;
  

  remarques : La propagation des états ainsi que la rétropropagation s'effectuent avec des opérations matricielles. Il est important de bien comprendre la structure des variables manipulées. Noter en particulier la différence entre la multiplication matricielle '*' et la multiplication scalaire (terme à terme) ' .*'. Comparer avec les formules littérales données dans la première partie du sujet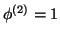.