


Next: Programmation des réseaux de
Up: Programmer des Réseaux neuronaux
Previous: Programmer des Réseaux neuronaux
Considérons un réseau en couches, tel que la mise à jour du
neurone de la couche 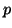 dépend des états des neurones de la
couche
dépend des états des neurones de la
couche 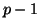 . Si la couche
. Si la couche 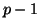 comporte
comporte 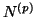 neurones, la
mise à jour de l'état d'activation
neurones, la
mise à jour de l'état d'activation 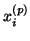 du
neurone
du
neurone
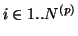 obéit à l'équation :
obéit à l'équation :
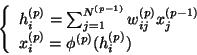 |
(1) |
Où 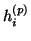 est le potentiel d'activation et les
est le potentiel d'activation et les
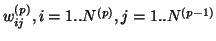 sont les connexions
synaptiques de la couche
sont les connexions
synaptiques de la couche 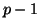 vers la couche
vers la couche 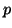 . La fonction
d'activation de la couche
. La fonction
d'activation de la couche 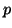 est
est 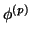 .
On considère l'apprentissage ``supervisé'' à partir d'une base
d'exemples constituée d'un ensemble d'entrées
.
On considère l'apprentissage ``supervisé'' à partir d'une base
d'exemples constituée d'un ensemble d'entrées
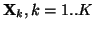 et d'un ensemble de sorties souhaitées associées à ces
entrées
et d'un ensemble de sorties souhaitées associées à ces
entrées
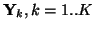 .
.

Cet algorithme permet entre autres d'approcher toute fonction
définie sur un compact de 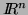 avec la précision
souhaitée (régression). En particulier, le réseau est
capable de généralisation, c'est à dire de produire des
sorties adéquates pour des entrées n'appartenant pas à la
base d'exemples. Néanmoins, cette propriété ne permet pas de
déterminer le nombre de couches cachées ni le nombre de
neurones dans les couches cachées. Dans le cadre de ce TP, on
utilisera un réseau avec 3 couches (une couche d'entrée, une
couche cachée, une couche de sortie).
avec la précision
souhaitée (régression). En particulier, le réseau est
capable de généralisation, c'est à dire de produire des
sorties adéquates pour des entrées n'appartenant pas à la
base d'exemples. Néanmoins, cette propriété ne permet pas de
déterminer le nombre de couches cachées ni le nombre de
neurones dans les couches cachées. Dans le cadre de ce TP, on
utilisera un réseau avec 3 couches (une couche d'entrée, une
couche cachée, une couche de sortie).



Next: Programmation des réseaux de
Up: Programmer des Réseaux neuronaux
Previous: Programmer des Réseaux neuronaux
Dauce Emmanuel
2005-03-30
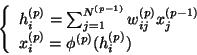

![]() avec la précision
souhaitée (régression). En particulier, le réseau est
capable de généralisation, c'est à dire de produire des
sorties adéquates pour des entrées n'appartenant pas à la
base d'exemples. Néanmoins, cette propriété ne permet pas de
déterminer le nombre de couches cachées ni le nombre de
neurones dans les couches cachées. Dans le cadre de ce TP, on
utilisera un réseau avec 3 couches (une couche d'entrée, une
couche cachée, une couche de sortie).
avec la précision
souhaitée (régression). En particulier, le réseau est
capable de généralisation, c'est à dire de produire des
sorties adéquates pour des entrées n'appartenant pas à la
base d'exemples. Néanmoins, cette propriété ne permet pas de
déterminer le nombre de couches cachées ni le nombre de
neurones dans les couches cachées. Dans le cadre de ce TP, on
utilisera un réseau avec 3 couches (une couche d'entrée, une
couche cachée, une couche de sortie).